Resumo
Este método se aproveita do Teorema do Valor Intermediário.
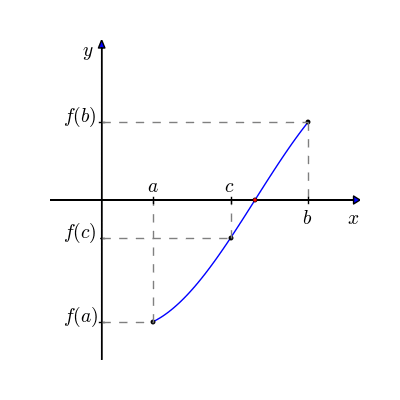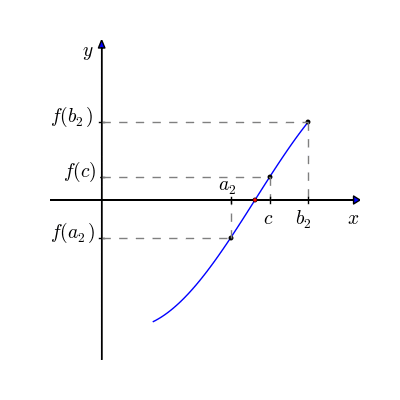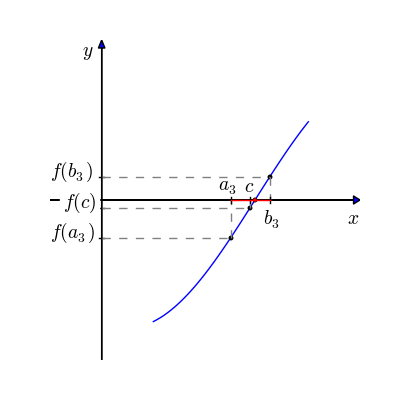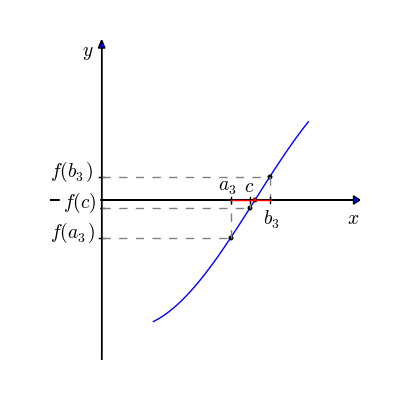
Se \(f(t)\) é uma função continua num intervalo fechado \([a, \ b]\) e \(f(a)\) e \(f(b)\) tiverem sinais opostos, então no intervalo \([a, \ b]\) existe pelo menos uma raiz.
A partir disso, cortamos o segmento \([a, \ b]\) no meio, e continuamos com o processo até termos uma boa aproximação da raiz:
Teoria
Nós sabemos que há pelo menos uma raiz no intervalo fechado \([a, \ b]\) devido ao Teorema do Valor Intermediário:
Erros
Restrições
- \(f(x)\) é contínua no intervalo fechado \([a, \ b]\)
- \(f(a)\) e \(f(b)\) devem ser de sinais opostos. Ou seja, \(f(a)\cdot f(b) < 0\)
Parametros
- Os valores de \(a\) e \(b\), em que \(a < b\)
- A função \(f(x)\), definida no intervalo \([a, \ b]\)
- O valor máximo \(n\) de iterações a fazer
- A tolerância \(tol\) à parar
Exemplo
Créditos e saiba mais
Aplicação
Caso a janela não abra, verifique se o AdBlock está impedindo isso.